Notes of Physics For Class 11th
Chapter 2 to Chapter 5
Chapter 2
Units and Measurements
Measurement of physical quantities
Physics is a quantitative science, based on measurement of physical quantities.Certain physical quantities have been chosen as fundamental or base quantities. The fundamental quantities that are chosen are Length, Mass, Time, electric current, thermodynamic temperature, amount of substance, and luminous intensity.
Base quantity and Fundamental Units
Each base quantity is defined in terms of a certain basic arbitrarily chosenbut properly standardised reference standard called unit (such as metre,kilogram,second,ampere,kelvin,mole,and candela.The units for the fundamental base quantities are called fundamental or base units and two supplementary units in relation to quantities plane angle and solid angle radian, Ste radian..
|
S.No. |
Fundamental Quantities |
Fundamental Units |
Symbol |
|
1. |
Length |
metre |
m |
|
2. |
Mass |
kilogram |
kg |
|
3. |
Time |
second |
S |
|
4. |
Temperature |
kelvin |
kg |
|
5 |
Electric current |
ampere |
A |
|
6 |
Luminous intensity |
candela |
cd |
|
7 |
Amount of substance |
mole |
mol |
Derived units
Other physical quantities derived from the base quantities can be expressed as a combination of the base units and are called derived units.A complete set of units both fundamental and derived units are called a system of units. Example :- volume, density etc
International System of units
*The International System of units based on seven base unitsis at present internationally acceptedunit system and is widely used throughout the world. In computing any physical quantity the units for derived quantities involved in the relationships are treated as though they were algebraic quantities till the desired units are obtained
- CGS System In this system, the unit of length is centimetre, the unit of mass is gram and the unit of time is second.
- FPS System In this system, the unit of length is foot, the unit of mass is pound and the unit of time is second.
- MKS System In this system, the unit of length is metre, the unit of mass is kilogram and the unit of time is second.
- SI System This system contain seven fundamental units and two supplementary fundamental units. The SI units are used in all physical measurements, for both the base quantitiesand the derived quantities obtained from them. Certain derived units are expressed by means of SI units of special names such as joule, newton, watt etc.
* In computing any physical quantity the units for derived quantities involved in the relationships are treated as though they were algebraic quantities till the desired units are obtained
* In SI system that is System Internationale d’ Units there are 7 base units’ andtwo supplementary units.
|
S.No. |
Supplementary Fundamental Quantities |
Supplementary Unit |
Symbol |
|
1 |
Plane angle |
radian |
rad |
|
2 |
Solid angle |
steradian |
Sr |
* Direct and indirect methods can be used for the measurement of physical quantities. In measured quantities while expressing theresult, the accuracy and precision of measuring instrumentsalong with errors in measurement should be taken into account.
* In measured and computed quantitiesproper significant figures only should be retained.
Use of Dimensional analysis
* The dimensions of base quantities and combination of these dimensions describe the nature of physical quantities .Dimensional analysis can be used to check the dimensional consistency of equations, deducing relations among physical quantities etc. A dimensionally consistent equation need not be actually an exact equation, but a dimensionally wrong or inconsistent equation must be wrong.
Error
The uncertainty in the measurement of a physical quantity is called an error.
The errors in measurement can be classified as (i) Systematic errors and (ii) Random errors
SYSTEMATIC ERRORS:
These are the errors that tend to be either positive or negative.Sources of systematic errors are
(i) Instrumental errors
(ii) Imperfection in experimental technique or procedure
(iii) Personal errors
RANDOM ERRORS :
Those errors which occur irregularly .These errors arise due to unpredictable fluctuations in experimental conditions
Least count error
Least count error is the error associated with the resolution of the instrument.
Absolute error
The magnitude of the difference between the individual measurement and the true value of the quantity is called the absolute error of the measurement.
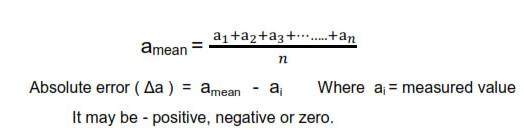
Mean Absolute Error
The arithmetic mean of all the absolute errors is taken as the final or mean absolute error of the value of the physical quantity a. It is represented by Δa mean
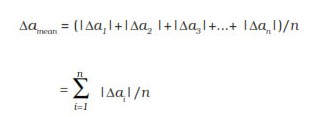
Relative error - it is the ratio of the mean absolute error to the true value.
Relative error = Δa mean/ a mean
Percentage Error : When the relative error is expressed in per cent, it is called the percentage error (δa).
Percentage error =( Δa mean/ a mean) ×100
COMBINATION OF ERRORS
ERROR OF A SUM OR A DIFFERENCE
When two quantities are added or subtracted, the absolute error in the final result is thesums of the absolute errors in the individual quantities.
IF Z=A+ B then the max possible error in Z, ∆Z =∆A + ∆B
IF Z=A- B then the max possible error in Z, ∆Z =∆A + ∆B
ERROR OF A PRODUCT OR A QUOTIENT
When two quantities are multiplied or divided the relative error is the sum of the relative errors in the multipliers
Suppose Z= A*B or Z=A/B then the max relative error in ‘Z’ = ∆Z/Z= (∆A/A) + (∆B/B)
ERROR IN CASE OF A QUANTITY RAISED TO A POWER
The relative error in a physical quantity raised to the power k is the k times the relative
error in the individual quantity.
Suppose Z = Ak
then ∆Z/Z = K (∆A/A)
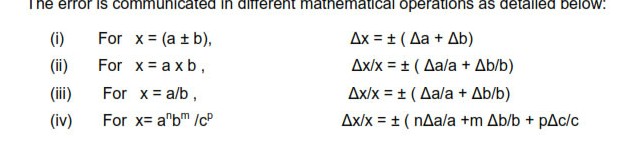
Significant figures
The significant figures are normally those digits in a measured quantity which are known reliably plus one additional digit that is uncertain.
For counting of the significant figure rule are as:
(i) All non- zero digits are significant figure.
(ii) All zero between two non-zero digits are significant figure.
(iii) All zeros to the right of a non-zero digit but to the left of an understood decimal point are not significant. But such zeros are significant if they come from a measurement.
(iv) All zeros to the right of a non-zero digit but to the left of a decimal point are significant.
(v) All zeros to the right of a decimal point are significant.
(vi) All zeros to the right of a decimal point but to the left of a non-zero digit are not significant. Single zero conventionally placed to the left of the decimal point is not significant.
(vii) The number of significant figures does not depend on the system of units.
Addition or subtraction with significatn figure :-
In addition or subtraction , the result should be reported to the same number of decimal places as that of the number with minimum number of decimal places.
For ex: A= 334.5 kg; B= 23.45Kg then A + B =334.5 kg + 23.43 kg = 357.93 kg
The result with significant figures is 357.9 kg
Mutiplication and division in significant figure :-
In multiplication or division, the result should be reported to the same number of significant figures as that of the number with minimum of significant figures.
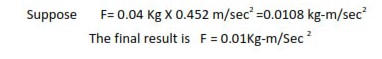
Accuracy in measurement
Accuracy refers to the closeness of a measurement to the true value of the physical quantity and precision refers to the resolution or the limit to which the quantity is measured. The accuracy of a measurement is a measure of how close the measured value is to the true value of the quantity.
Precision
Precision tells us to what limit the quantity is measured.
ROUNDING OFF:
While rounding off measurements the following rules are applied
Rule I: If the digit to be dropped is smaller than 5,then the preceding digit should be left unchanged. For ex: 9.32 is rounded off to 9.3
Rule II: If the digit to be dropped is greater than 5, then the preceding digit should be raised by 1 For ex: 8.27 is rounded off to 8.3
Rule III: If the digit to be dropped is 5 followed by digits other than zero, then the preceding digit should be raised by 1
For ex: 9.351 on being rounded off to first decimal, becomes 9.4
Rule IV: If the digit to be dropped is 5 or 5 followed by zeros, then the preceding digit is not changed if it is even, is raised by 1 if it is odd. For ex:
5.45, on being rounded off,become 5.4
5.450 on being rounded off, becomes 5.4
7.35 , on being rounded off, becomes 7.4
DIMENSIONS, DIMENSIONAL FORMULA AND DIMENSIONAL EQUATION
(1)Dimensions of a derived unit are the powers to which the fundamental units of mass, length
and time etc. must be raised to represent that unit.
(2)Dimensional formula is an expression which shows how and which of the fundamental units
are required to represent the unit of a physical quantity.M1L1T-2 is the dimensional formula of Force.
CATEGORIES PHYSICAL QUANTITIES
Dimensional Costants: These are the quantities which possess dimensions and have a fixed value.
Ex: Gravitational Constant
Dimensional Variables: These are the quantities which possess dimensions and do not have a fixed value
For ex: velocity, acceleration etc.
Dimensionless Constants: these are the quantities which do not possess dimensions and have a fixed value.
For ex: πetc.
Dimensionless Variables: These are the quantities which are dimensionless and do not have a fixed value.
For ex: Strain, Specific Gravity etc.
Importance of dimentional analysis
A given physical relation is dimensionally correct if the dimensions of the variousterms on either side of the relation are the same.
USES OF DIMENSIONAL EQUATIONS

LIMITATIONS OF DIMENSIONAL ANALYSIS
* It supplies no information about dimensionless constants. They have to be determined either by experiment or by mathematical investigation.
* This method applicable only in the case of power functions. It fails in case of
exponential and trigonometric relations.
* It fails to derive a relation which contains two or more than two quantities of like nature.
* It can only check whether a physical relation is dimensionally correct or not. It cannot tell whether the relation is absolutely correct or not
* It cannot identify all the factors on which the given physical quantity depends upon.
Chapter 3
Motion in a straight
Motion:-
Rest and Motion are relative terms, nobody can exist in a state of absolute rest or of absolute motion.
One dimensional motion:-
The motion of an object is said to be one dimensional motion if only one out of three coordinates specifying the position of the object change with time. In such a motion an object move along a straight line path.
Two dimensional motion
The motion of an object is said to be two dimensional motion if two out of three coordinates specifying the position of the object change with time. In such motion the object moves in a plane.
Three dimensional motion:-
The motion is said to be three dimensional motion if all the three coordinates specifying the position of an object change with respect to time ,in such a motion an object moves in space.
Path length :-
The path length traversed by an object between two points is not the same as the magnitude of displacement always. The displacement depends only on the end points; whereas the path length depends on the actual path. The two quantities are equal only if the object does not change its direction during the course of its motion. In all other cases, the path length is greater than the magnitude of displacement.
Average speed :-
The average speed of an object is greater than or equal to the magnitude of the averagevelocity over a given interval of time. The two are equal only if the path length is equal to the magnitude of the displacement.
Displacement
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P. A displacement vector represents the length and direction of this imaginary straight path.
The magnitude of displacement is less than or equal to the actual distance travelled by the object in the given time interval.
Displacement ≤ Actual distance
Speed
It is rate of change of distance covered by the body with respect to time.
Speed = Distance travelled /time taken
Speed is a scalar quantity .
Its unit is meter /sec.
Dimensional formula of speed is [M0L1 T -1 ] .
It is positive or zero but never negative.
Uniform Speed:-
If an object covers equal distances in equal intervals of time than the speed of the moving object is called uniform speed. In this type of motion, position – time graph is always a straight line.
Instantaneous speed:-
The speed of an object at any particular instant of time is called instantaneous speed. In this measurement, the time ∆t→0. When a body is moving with uniform speed its instantaneous speed = Average speed = uniform speed.
Velocity
The rate of change of position of an object in a particular direction with respect to time is called velocity. It is equal to the displacement covered by an object per unit time.
Velocity =Displacement /Time
Velocity is a vector quantity
its SI unit is meter per sec.
Its dimensional formula is [M0L1 T -1 ].
It may be negative, positive or zero.
When a body moves in a straight line then the average speed and average velocity are equal.
Acceleration
The rate of change of velocity of an object with respect to time is called its acceleration.
Acceleration = Change in velocity /time taken
It is a vector quantity,
Its SI unit is meter/ sec2
Its dimension is [M0L1 T -2 ].
It may be positive ,negative or zero.
Positive Acceleration:-
If the velocity of an object increases with time, its acceleration is positive .
Negative Acceleration :-
If the velocity of an object decreases with time, its acceleration is negative . The negative acceleration is also called retardation or deacceleration.
Formulas of uniformly accelerated motion along straight line

Free fall :-
In the absence of the air resistance all bodies fall with the same acceleration towards earth from a small height. This is called free fall. The acceleration with which a body falls is called gravitational acceleration (g).Its value is 9.8 m/sec2 .
Relative Motion:-
The rate of change of distance of one object with respect to the other is called relative velocity. The relative velocity of an object B with respect to the object A when both are in motion is the rate of change of position of object B with respect to the object A.
Relative velocity of object A with respect to object B, VAB = VA - VB
When both objects are move in same direction, then the relative velocity of object B with respect to the object A,
VBA = VB - VA
When the object B moves in opposite direction of object A .
VBA = VB + VA
Chapter 4
motion in a plane
Scalar Quanties:-
The quantities which have magnitude only but no direction. For example : mass, length, time, speed , temperature etc.
Vector Quantities :-
The quantities which have magnitude as well as direction and obeys vector laws of addition, multiplication etc. For examples : Displacement, velocity, acceleration, force , momentum etc.
Addition of Vectors :-
(i) Only vectors of same nature can be added.
(ii) The addition of two vector A and B is resultant R
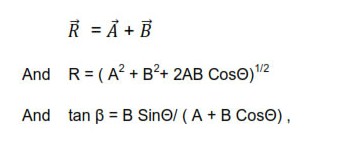
Where Θ is the angle between vector A and vector B, And β is the angle which R makes with the direction of A.
(iii) Vector addition is commutative A + B = B+A
(iv) Vector addition is associative,A+ (B +C ) = (A +B )+C
(v) R is maximum if Θ = 0 and minimum if Θ = 180 + 0 .
Subtraction of two vectors :-
(i) Only vector of same nature can be subtracted.
(ii) Subtraction of B from A = vector addition of A and (-B),

Where Θ is the angle between A and B and β is the angle which R makes with the direction of A.
(iii) Vector addition is commutative A + B ≠ B+A
(iv) Vector addition is associative,A+ (B +C ) ≠ (A +B )+C
Rectangular components of a vector in a plane :-
If A makes an angle Θ with x-axis and Ax and By be the rectangular components of A along X-axis and Y- axis respectively.
Then A= A x + By= y
Here A x =A CosΘ and B y = ASinΘ
Dot product or scalar product : -
The dot product of two vectors A and B, represented by . is a scalar , which is equal to the product of the magnitudes of A and B and the Cosine of the smaller angle between them. If Θ is the smaller angle between A and B, then AB= AB
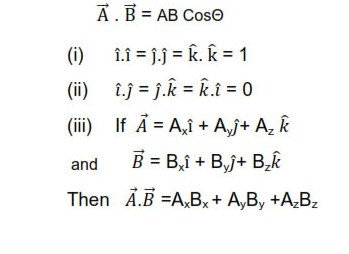
Cross or Vector product :-
The cross product of two vectors and , represented by x is a vector , which is equal to the product of the magnitudes of A and B and the sine of the smaller angle between them. If Θ is the smaller angle between A and B, then = AB Sinθ

Projectile motion : -
Projectile is the name given to anybody which once thrown in to space with some initial velocity, moves thereafter under the influence of gravity alone without being propelled by any engine or fuel. The path followed by a projectile is called its trajectory.

CIRCULAR MOTION
Circular Motion –
When a body moves such that it always remains at a fixed distance from a fixed point then its motion is said to be circular motion. The fixed distance is called the radius of the circular path and the fixed point is called the center of the circular path.
Uniform circular motion:-
When an object follows a circular path at constant speed. The motion of the object is called uniform circular motion.
The magnitude of its acceleration is a c = v2/R.
The direction of a c is always towards the centre of the circle.
Angular Displacement –
Angle swept by the radius vector of a particle moving on a circular path is known as angular displacement of the particle. Example :– angular displacement of the particle from P1 to P2 is θ.

Angular speed :-
The angular speed is the rate of change of angular distance.
It is related velocity v by V =ω R. The acceleration is ac= ω2R.
If T is the time period of revolution of the object in circular motion and ν is the frequency then we have ω = 2πνV = 2πνR and acceleration a= 4π2 ν 2 R

Instantaneous Angular Velocity –
Angular velocity of a body at some particular instant of time is known as instantaneous angular velocity.
Or
Average angular velocity evaluated for very short duration of time is known as instantaneous angular velocity.

Time Period of Uniform Circular Motion –
Total time taken by the particle performing uniform circular motion to complete one full circular path is known as time period. In one time period total angle rotated by the particle is 2π and time period is T. Hence angular velocity
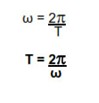
Frequency -
Number of revolutions made by the particle moving on circular path in one second is known as frequency.
f = 1/T = ω/2π
Centripetal Acceleration –
When a body performs uniform circular motion its speed remains constant but velocity continuously changes due to change of direction. Hence a body is continuously accelerated and the acceleration experienced by the body is known as centripetal acceleration (that is the acceleration directed towards the center).
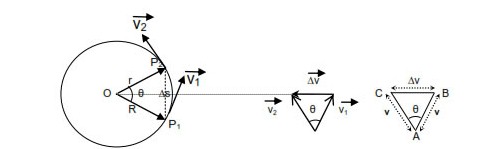
Consider a particle performing uniform circular motion with speed v. When the particle changes its position from P1 to P2. its velocity changes from v1 to v2 due to change of direction. The change in velocity from P1 to p2is ∆v which is directed towards the center of the circular path according to triangle law of subtraction of vectors.
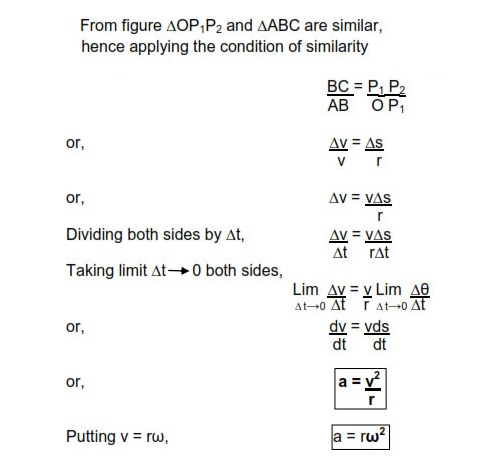
Since the change of velocity is directed towards the center of the circular path, the acceleration responsible for the change in velocity is also directed towards center of circular path and hence it is known as centripetal acceleration.
Centripetal force :-
Centripetal force is the name given to the force that provides inward radial acceleration to a body in circular motion.We should always look for some materia lforce like tension, gravitational force, electrical force, frictionetc. as the centripetal force.
Physical Application of Centripetal Force
i)Case - 1 Circular motion of a stone tied to a string. Centripetal force is provided by the tension of the string
- ii) Case - 2 Circular motion of electron around the nucleus. Centripetal force is provided by the electrostatic force of attraction between thepositively charged nucleus and negatively charged electron
iii) Case - 3 Circular motion of planets around sun or satellites around planet. Centripetal force is provided by the gravitational force of attraction between the planet and sun
- iv) Case - 4 Circular motion of vehicles on a horizontal road. Centripetal force is provided by the static frictional force between the road and the tyre of the vehicle.
- vi) Case - 6 Circular motion of mud particles sticking to the wheels of the vehicle. Centripetal force is provided by the adhesive force of attraction between the mudparticles and the tyres of the vehicle. At very high speed when adhesive force is unable to provide necessary centripetal force, the mud particles fly off tangentially. In order to prevent the particles from staining our clothes, mud-guards are provided over the wheels of vehicle.
vii) Case - 7 Circular motion of a train on a horizontal track. Centripetal force is provided by the horizontal component of the reaction force applied by the outer track on the inner projection of the outer wheels
Notes of physics FSc Part1 Part A
Notes of Physics For FSC Part1 Part B
Notes of Physics For FSC Solved Problems
FSc Part 2nd Physics Solved Exercises
FSc Part 2nd Physics Solved Exercises Chapter 3
FSc Part 2nd Physics Solved Exercises Chapter 4
FSc Part 2nd Physics Solved Exercises Chapter 5
Notes of Urdu for FA Ch-1 to Ch-4
Notes of Urdu for FA Ch-5 to Ch-7
Notes of Urdu for FA Ch-8 to Ch-13
Notes of Principles of Economics 1st year
Notes of Physics FSc Part 2nd (Electrostatics)
Notes of English For FA/Fsc Part 1st (Section-A)
Notes of English For FA/Fsc Part 1st (Section-B)
Notes of English For FA/Fsc Part 1st (Section-C)